Arytmetyczna czy ważona?

Idziesz do sklepu, aby kupić 5 kg ziemniaków i 2 kg buraków. Na początku jednak wkładasz do koszyka trzy inne produkty: batonik za 2,6 zł, herbatniki za 3,3 zł i napój za 2,8 zł. Jaka jest średnia cena jednego produktu?

Ten wynik oznacza, że jeśli każdy z produktów kosztowałby 2,9 zł, to za trzy należałoby zapłacić 8,7 zł. Właśnie policzyliśmy średnią arytmetyczną. Jest to najczęściej wykorzystywana miara statystyczna. Kiedy słyszysz lub mówisz słowo „średnia”, to najczęściej chodzi właśnie o średnią arytmetyczną. Liczymy ją w ten sposób, że sumujemy wszystkie wartości, a następnie dzielimy otrzymaną sumę przez liczbę tych wartości, jak w powyższym przykładzie.

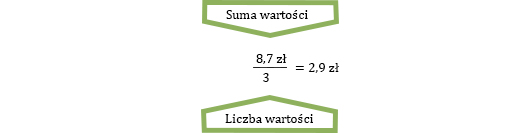
W ten sposób można obliczyć średnią właściwie wszystkiego: średnią cenę produktu, średni wzrost, średnią liczbę teatrów w miastach wojewódzkich, średnią liczbę osób w rodzinie itd. Jak każda miara, średnia nie jest idealna. Liczenie średniej daje czasem wyniki, które mogą wydawać się dziwne lub śmieszne – na przykład, że w rodzinie jest średnio 2 i ½  osoby. Jak to ½ osoby?

W niektórych sytuacjach statystycy korzystają również z innych miar niż średnia arytmetyczna. O niektórych dowiesz się w kolejnych artykułach.

Wróćmy do naszych zakupów. Po takiej ilości słodyczy musisz uzupełnić witaminy i mikroelementy. Na kolejnym stoisku kupujesz więc owoce na sztuki: jabłko za 1 zł, gruszkę za 1,5 zł i banana za 2 zł. Już teraz na pewno z łatwością policzysz średnią arytmetyczną. Wynik możesz sprawdzić tutaj.

Podczas liczenia średniej bardzo ważna jest liczba wartości, dla których liczysz średnią. Załóżmy, że wkładasz do koszyka jeszcze jedno jabłko. Teraz w koszyku masz cztery owoce. Czy średnia cena owocu (spośród tych, które masz w koszyku) zmieniła się? Tak. Musisz to uwzględnić podczas obliczeń.

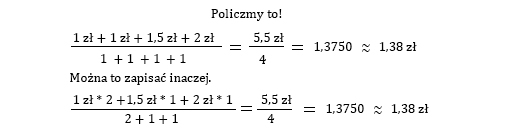
W tym drugim wzorze w liczniku najpierw pomnożyliśmy przez siebie cenę (wartość) i liczbę wystąpień tej ceny (ile owoców danego rodzaju mamy w koszyku), np. cena jabłka 1 zł * 2 jabłka. W mianowniku zaś zsumowaliśmy liczbę owoców. Wynik oznacza, że jeśli każdy z owoców kosztowałby 1,38 zł, to na zakup czterech należałoby wydać 5,5 zł.

Liczby owoców w tym wzorze to wagi naszych wartości. Wartości, którym przypisane są większe wagi mają większy udział w obliczaniu średniej niż dane z mniejszymi wagami. W naszym przykładzie jabłka mają większą wagę (2) niż gruszki (1) i banany (1). Taka średnia to średnia ważona.

Liczymy ją w ten sposób, że każdą wartość mnożymy przez wagę (w naszym przykładzie cenę mnożymy przez liczbę owoców) i sumujemy wyniki mnożenia – tak otrzymujemy licznik ułamka. Następnie sumujemy wszystkie wagi (w naszym przykładzie liczbę owoców) – tak otrzymujemy mianownik ułamka. Na koniec wykonujemy dzielenie i otrzymujemy średnią ważoną.

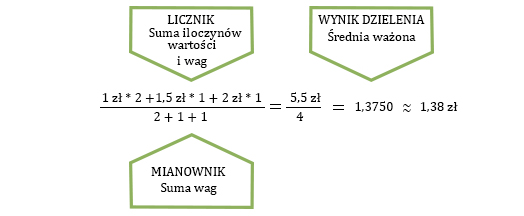
Zrozumienie różnicy między średnią arytmetyczną a średnią ważoną może na początku sprawić trochę trudności. Spójrz na kolejny przykład.

Wreszcie docierasz do stoiska z warzywami i wkładasz do koszyka 5 kg ziemniaków i 2 kg buraków, w sumie 7 kg warzyw. Cena ziemniaków wynosi 2 zł/kg, a buraków 4 zł/kg. W sumie zapłacisz więc za warzywa 18 zł.

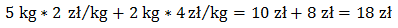
 A jaka będzie średnia cena 1 kg warzyw, które masz w koszyku?

Jeśli policzysz zwykłą średnią arytmetyczną z dwóch cen, to otrzymasz wynik 3 zł/kg.

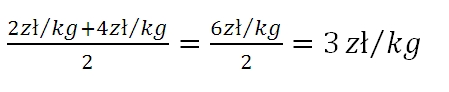
To oznaczałoby, że jeśli każdy kilogram warzyw kosztowałby 3 zł/kg, to 7 kg kosztowałoby 21 zł. A Ty zapłacisz 18 zł. Coś się nie zgadza! Wynik jest błędny, ponieważ nie uwzględniłeś liczby kilogramów.

Żeby obliczyć średnią cenę musisz podzielić kwotę, którą zapłacisz przez liczbę zakupionych kilogramów. Liczby kilogramów będą wagami, które należy wstawić do wzoru.​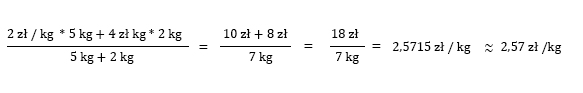

Średnia ważona

Jedziesz ze swoją klasą na szkolną wycieczkę do muzeum. Mieliście do przejechania 100 km. Połowę drogi przejechaliście z prędkością 100 km/godz., ale drugą połowę drogi z powodu robót drogowych przejechaliście z prędkością 25 km/godz. Jaka była Wasza średnia prędkość?

Jeśli policzysz zwykłą średnią arytmetyczną z dwóch wartości prędkości jazdy, to otrzymasz wynik 62,5 km/godz. A to błąd!

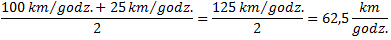
Żeby obliczyć średnią prędkość jazdy w km/godz. musisz podzielić liczbę kilometrów, którą przejechaliście przez liczbę godzin, którą to Wam zajęło.

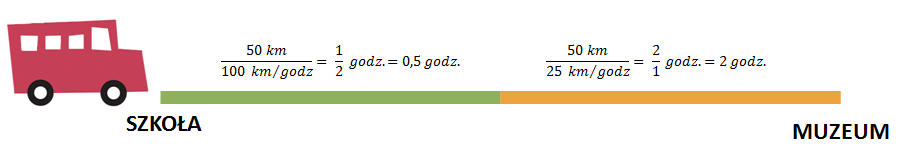
Pierwszą połowę drogi, czyli 50 km, przejechaliście z prędkością 100 km/godz., a więc zajęło to 0,5 godz. Drugą połowę drogi, czyli kolejne 50 km przejechaliście z prędkością 25 km/godz., a więc zajęło to Wam 2 godziny. I takie dane trzeba podstawić do wzoru. Podczas obliczania średniej prędkości jazdy należy więc skorzystać ze wzoru na średnią ważoną.

Prędkość jest naszą wartością, a liczba godzin będzie wagą, którą przypiszemy do prędkości.

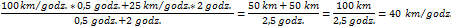
W ten sposób wiemy, że przejechaliście całą trasę ze średnią prędkością
40 km/godz.

Średnia, mediana, rozstęp

Jesteśmy kibicami na zawodach lekkoatletycznych. W biegu na 100 m uczestniczyło 5 zawodników. Osiągnęli następujące czasy:

Zawodnik z nr 1: 12,89 s

Zawodnik z nr 2: 15,72 s

Zawodnik z nr 3: 11,54 s

Zawodnik z nr 4: 12,56 s

Zawodnik z nr 5: 13,01 s

Możemy powiedzieć, że zawodnicy, którzy uczestniczyli w biegu to nasza badana zbiorowość. Cecha, którą będziemy badać, to czas w sekundach, w którym zawodnicy przebiegli 100 m.

Na początek uszeregujemy wyniki, czyli ułożymy je w kolejności od najmniejszej do największej.

Dzięki temu wiemy, kto pobiegł najlepiej, a kto najsłabiej. Najmniejsza uzyskana wartość – czyli najkrótszy czas w sekundach na 100 m: 11,54 s, to minimum, a największa uzyskana wartość – czyli najdłuższy czas: 15,72 s – to maksimum. Oczywiście w przypadku biegu najlepszy czas to czas najkrótszy, a więc minimum. W ten sposób poznajemy dwie wartości, które opisują nam zbiorowość: minimum i maksimum.

Jeśli mamy minimum i maksimum możemy obliczyć rozstęp, czyli różnicę między maksimum i minimum.

MAX – MIN = ROZSTĘP

15,72 s – 11,54 s = 4,18 s

A jaki był średni czas, w którym zawodnicy pokonali dystans 100 m w tym biegu? Odpowiedź na to pytanie wymaga od nas nieco więcej liczenia. Najpopularniejszą średnią jest średnia arytmetyczna. Liczymy ją w ten sposób, że dodajemy wszystkie wartości, a następnie dzielimy otrzymaną sumę przez liczbę tych wartości.

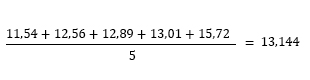
A więc średni czas w sekundach zawodników w biegu na 100 m to 13,144 sekundy.

Więcej o średniej arytmetycznej i nie tylko dowiesz się w artykule „Arytmetyczna czy ważona?”.

Inną wartością, która może nam powiedzieć o tym, jaka była przeciętna (średnia) wartość badanej cechy jest mediana. Medianę bardzo łatwo wskazać – jest to wartość środkowa w naszym uszeregowanym zbiorze danych.

Mediana dzieli nam zbiór danych na połowę: tyle samo wartości jest mniejszych od mediany i tyle samo wartości jest większych od mediany.

Być może już to widzisz, że w naszym przykładzie wskazanie mediany nie stanowi problemu, ponieważ mamy nieparzystą liczbę danych. A co, jeśli zawodników byłoby sześcioro? Którą wartość wybrać?

Wtedy bierzemy dwie środkowe wartości i liczymy z nich średnią arytmetyczną.

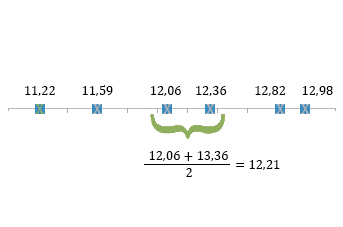
Wszystkie liczby, które wyznaczyliśmy w tym przykładzie to miary statystyczne, czyli różnego rodzaju wartości liczbowe obliczane na podstawie danych statystycznych.

Dlaczego warto liczyć różne miary?

W ten sposób poznajesz badaną zbiorowość, możesz zauważyć różne prawidłowości i odwrotnie – sytuacje nieprawidłowe, nietypowe. Możesz również zaobserwować, czy wyniki zmieniają się i jak się zmieniają w zależności od miejsca, gdzie były zbierane dane (np. miasto, wieś, różne kraje) czy czasu, w którym były zbierane (np. miesiąc, rok, wiek).

Dzięki liczeniu różnych miar możesz również dokonywać porównań. Załóżmy, że na lekcji w-f zmierzono czas na dystansie 100 m dwudziestu uczniom – dziesięciu z klasy A i dziesięciu z klasy B. Spójrzmy, jakie średnie czasy uzyskali uczniowie.

Średnie arytmetyczne nie różnią się tak bardzo. To by oznaczało, że średni poziom obydwu klas jest bardzo podobny. Spójrzmy jednak na inne miary.

Jak widzisz w klasie A wynik najlepszy (czyli najkrótszy czas) jest wyraźnie mniejszy niż w klasie B, a z drugiej strony wynik najgorszy (czyli najdłuższy czas) jest znacznie gorszy niż w klasie B. To oznacza, że rozstęp jest większy dla klasy A niż dla B. 

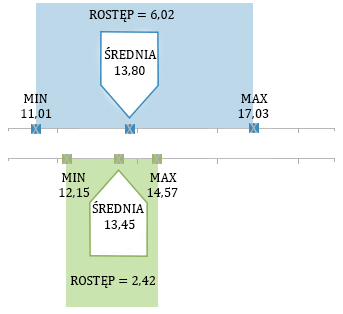
Jakie mogą być powody takich wyników? Wartości rozstępu mogą wskazywać na to, że w klasie B poziom wszystkich uczniów jest bardziej wyrównany – nie ma tam uczniów szczególnie wyróżniających się – ani znacznie gorszych niż inni, ani znacznie lepszych. Z kolei w klasie A są uczniowie (albo przynajmniej jeden uczeń) sporo słabsi od reszty, ale też są uczniowie (albo przynajmniej jeden uczeń) sporo lepsi. Żeby się dowiedzieć, ilu uczniów jest znacznie gorszych lub znacznie słabszych, musisz przyjrzeć się uszeregowanym wynikom poszczególnych uczniów.

Wyobraź sobie, że szukasz zawodnika, który ma reprezentować całą szkołę na zawodach lekkoatletycznych. Czy będzie to uczeń z klasy A czy B?

Jeśli szukalibyśmy jednego ucznia, który ma największe szanse na zawodach lekkoatletycznych, to zdecydowanie powinnyśmy szukać w klasie A.

Zagraj i poćwicz liczenie średniej, mediany i rozstępu!